Adaptive Spatial Goodness Encoding in Machine Learning

该算法结构模仿VGG的Block思想，提出了带有Adaptive Spatial Goodness Encoding的Block模块：

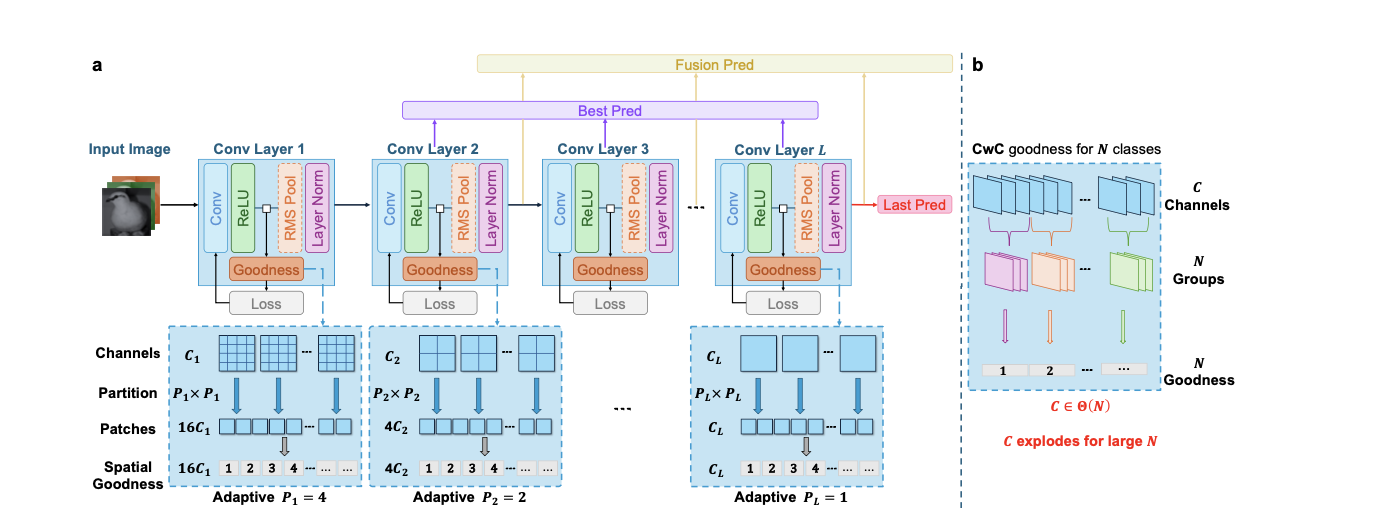
Block Structure

输入X_i为多通道矩阵数据(H, W, c)
Convolution → ReLU → RMS Pool → Layer Norm

RMS Pool

$X: (H, W, C) → Y1: (H/s, W/s, C)$ 其中，对于每个池化窗口$s\times s$,计算

$$ \mathbf{Y}{RMS}^{(i,j,c)} = \sqrt{\frac{1}{HW} \sum{h=1}^{H} \sum_{w=1}^{W} \left(\mathbf{X}^{(i+h, j+w, c)}\right)^2} $$

Layer Normalization

$$ \text{LayerNorm}(\mathbf{x}) = \gamma \odot \frac{\mathbf{x} - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta $$

$$ \mu = \frac{1}{D} \sum_{i=1}^{D} x_i ; ; ; \sigma^2 = \frac{1}{D} \sum_{i=1}^{D} (x_i - \mu)^2 $$

常量 γ (scale): 尺度参数，初始化为1 β (shift): 偏移参数，初始化为0 ε: 数值稳定项（如 1e-5）形状保持不变，LayerNorm在通道维度 C 上进行归一化。

Adaptive Spatial Goodness Encoding算法

对于第$l$层的预测结果$Y_l($针对X输入至Conv + ReLu),对其进行Goodness编码，并基于编码实现本地的参数更新。对于Y_l（W_l, H_l, c_l）我们对每一个channel的二维矩阵分割为若干p_l*p_l大小的区块，定义:

$$ P_l = \min\left(\max\left(1, \left\lfloor\alpha \cdot \frac{C_L}{C_l}\right\rfloor\right), H_l, W_l\right) $$

变量说明：

$P_l$：第 $l$ 层的空间分割因子（每个维度的patch数量）
$C_l$：第 $l$ 层的通道数
$C_L$：最后一个卷积层的通道数
$\alpha \geq 0$：超参数，控制分割粒度（论文中 $\alpha=1$ 效果最佳）
$H_l, W_l$：第 $l$ 层的空间维度

设计原理：浅层（$C_l$ 小）→ $P_l$ 大 → 更细粒度的空间分割；深层（$C_l$ 大）→ $P_l$ 小 → 更粗粒度的空间分割，进而得到 $P_l \times P_l \times C_l$ 个区块，对于每一个区块都有一个goodness评估值中$c \in {1, 2, \ldots, C_l}$为通道索引，$i, j \in {1, 2, \ldots, P_l}$为patch的空间位置索引

Goodness 计算公式：

$$ g_{l,c}^{(i,j)} = \frac{1}{H’_l W’l} \sum{h=1}^{H’l} \sum{w=1}^{W’_l} \left(\tilde{Y}_l^{(c,i,j,h,w)}\right)^2 $$

其中：$H’_l = H_l / P_l$，$W’_l = W_l / P_l$：为单个patch内的空间尺寸；$\tilde{Y}_l \in \mathbb{R}^{C_l \times P_l \times P_l \times H’_l \times W’_l}$为分割后的每一个区块元素。计算区域平方和，可以看作每个patch的goodness衡量该局部区域的激活强度（能量），反映特征的显著性。

我们对 $(C_l \times P_l^2)$ 个goodness值 $\mathbf{g}$ 做flatten合并为一个向量，并做线性变换 $\mathbf{a}_l = \mathbf{W}_l \mathbf{g} + \mathbf{b}_l$，其中 $\mathbf{W}_l$ 和 $\mathbf{b}_l$ 在初始化后固定，$N$为类别数量。并使用$\mathbf{a}_l$计算局部交叉熵损失，使用$L_l$关于$\theta_l$的梯度更新这一个Block的参数

$$ \mathbf{W}_l \sim \mathcal{N}\left(0, \frac{1}{\sqrt{N}}\right), \quad \mathbf{b}_l \sim \mathcal{N}\left(0, \frac{1}{\sqrt{N}}\right) $$

在算法的流程上，每一次数据流经过Block，会并行完成两个过程，两个分支并行：X_l → Y_l → （分支1）流入RMS和LN进入下一个Block → （分支2）使用Y_l更新本地参数。

训练分类阶段策略

我们依然考虑模型前半部分为模式识别，大量使用ASGE Block；而模型后期为分类层，最简单的，使用Single Linear Linear实现分类：

$$ \hat{Y}{\text{Global}} = \mathbf{W}{\text{global}}\mathbf{z} + \mathbf{b}_{\text{global}} $$

这里给出三个Strategies：

Last Pred - 最后层预测

$$ \mathbf{z}_{\text{Last}} = \text{Flatten}\left(\text{GAP}(\mathbf{Y}_L)\right) $$

GAP：Global Average Pooling，对 $\mathbf{Y}_L$ 的空间维度做全局平均
特点：仅使用最后一层，分类器参数最少
适用场景：推理速度优先

Fusion Pred - 累积层融合预测

$$ \mathbf{z}_{\text{Fusion}} = \text{Concat}\left[\text{Flatten}(\text{GAP}(\mathbf{Y}_2)), \ldots, \text{Flatten}(\text{GAP}(\mathbf{Y}_L))\right] $$

跳过第一层：因其预测准确率太低
特点：
- 聚合多层特征，表达能力最强
- 分类器参数量最大：$\sum_{l=2}^{L} C_l$ 个输入特征
- 需要存储中间激活，内存开销较高
灵感来源：原始FF算法（Hinton 2022）的多层融合策略

Best Pred - 最佳层选择预测

$$ \mathbf{z}{\text{Best}} = \text{Flatten}\left(\text{GAP}(\mathbf{Y}{l^*})\right) $$

$$ \text{where} \quad l^* = \arg\max_{l \in {2, \ldots, L}} \text{ValidationAcc}_l $$

动态选择：在验证集上选择准确率最高的层
特点：
- 无需分类器：直接使用选中层的输出
- 支持Early Exit：推理时可在 $l^*$ 层提前终止，节省计算
- 内存零开销：无需存储其他层的激活
Trade-off：牺牲少量准确率（~1.74%）换取零参数和零内存

算法分析

1. 解决 FF 的深度退化问题

原始 FF 问题：深层准确率递减
ASGE 解决方案：通过空间 goodness 编码，深层准确率单调递增

2. 自适应的特征粒度匹配

$$ P_l = \alpha \cdot \frac{C_L}{C_l} $$

浅层（通道少）→ 细粒度分割 → 捕获局部细节
深层（通道多）→ 粗粒度分割 → 捕获全局语义
符合 CNN 的层次化特征抽象规律

3. 能量守恒的信息传递

RMS Pooling 保持激活能量不失真
Goodness（均方激活）与 RMS Pool 数学一致
相比 Max/Avg Pool，信息损失更小

4. 解耦通道数与类别数

$$ \text{Goodness 维度} = C_l \times P_l^2 \quad (\text{与类别数 } N \text{ 无关}) $$

CwC 问题：$C_l \propto N$，ImageNet (N=1000) 导致通道爆炸
ASGE 优势：$C_l$ 独立于 $N$，可扩展到大规模数据集

5. 局部监督 + 全局一致性

每层独立优化 → 并行训练，无梯度锁定
空间 goodness 提供丰富的局部信号
随机投影连接局部特征与全局标签

实验验证：CIFAR-100 上超越所有 FF 变体 12.33%，首次成功应用于 ImageNet