Introduction to ResNet

算法部署

Residual Block 结构

ResNet的核心创新在于引入了残差连接（Residual Connection），也称为跳跃连接（Shortcut Connection）。每个Residual Block的基本结构如下：

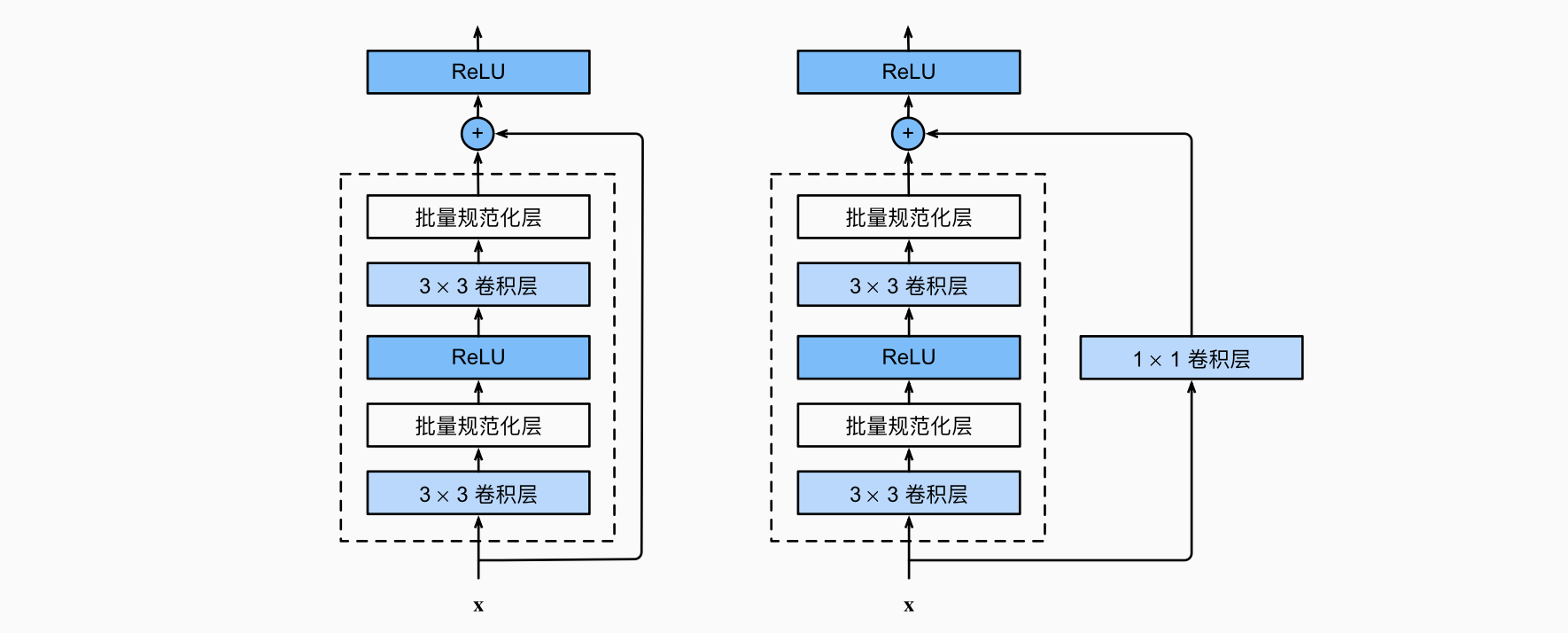
算法流程

数据流动过程：

1. 输入阶段：特征图 $x$ 进入Residual Block
2. 主路径处理：
   • $x$ 经过若干卷积层和激活函数的变换，得到 $F(x)$
   • 这部分称为残差函数（Residual Function）
3. 跳跃连接：
   • 原始输入 $x$ 通过恒等映射（Identity Mapping）直接传递
   • 如果维度匹配：直接传递
   • 如果维度不匹配：通过 $1 \times 1$ 卷积进行投影变换 $W_s x$
4. 特征融合：
   • 将残差函数输出 $F(x)$ 与跳跃连接输出相加
   • 数学表达：$y = F(x, {W_i}) + x$ 或 $y = F(x, \{W_i\}) + W_s x$
5. 激活输出：
   • 通过ReLU激活：$\sigma(y)$
   • 输出特征图传递到下一层

     实现细节

维度匹配策略：

• 选项A（零填充）：当维度增加时，用零填充额外的通道，不引入额外参数
• 选项B（投影）：使用 $1 \times 1$ 卷积进行投影匹配维度

• 选项C（全投影）：所有跳跃连接都使用投影
  下采样处理：

• 当特征图尺寸减半时，卷积步长设为2

• 通道数翻倍以保持每层的时间复杂度
  批归一化位置：

• 在每个卷积层之后、激活函数之前使用BN

---

算法原理分析

核心思想

ResNet的设计动机源于一个关键观察：更深的网络在训练时会出现退化问题（Degradation Problem）。令人意外的是，这种退化不是由过拟合引起的，而是由优化困难导致的。

退化问题的表现：

• 当网络加深时，训练误差反而增加
• 这说明深层网络很难学习到恒等映射（Identity Mapping）
  

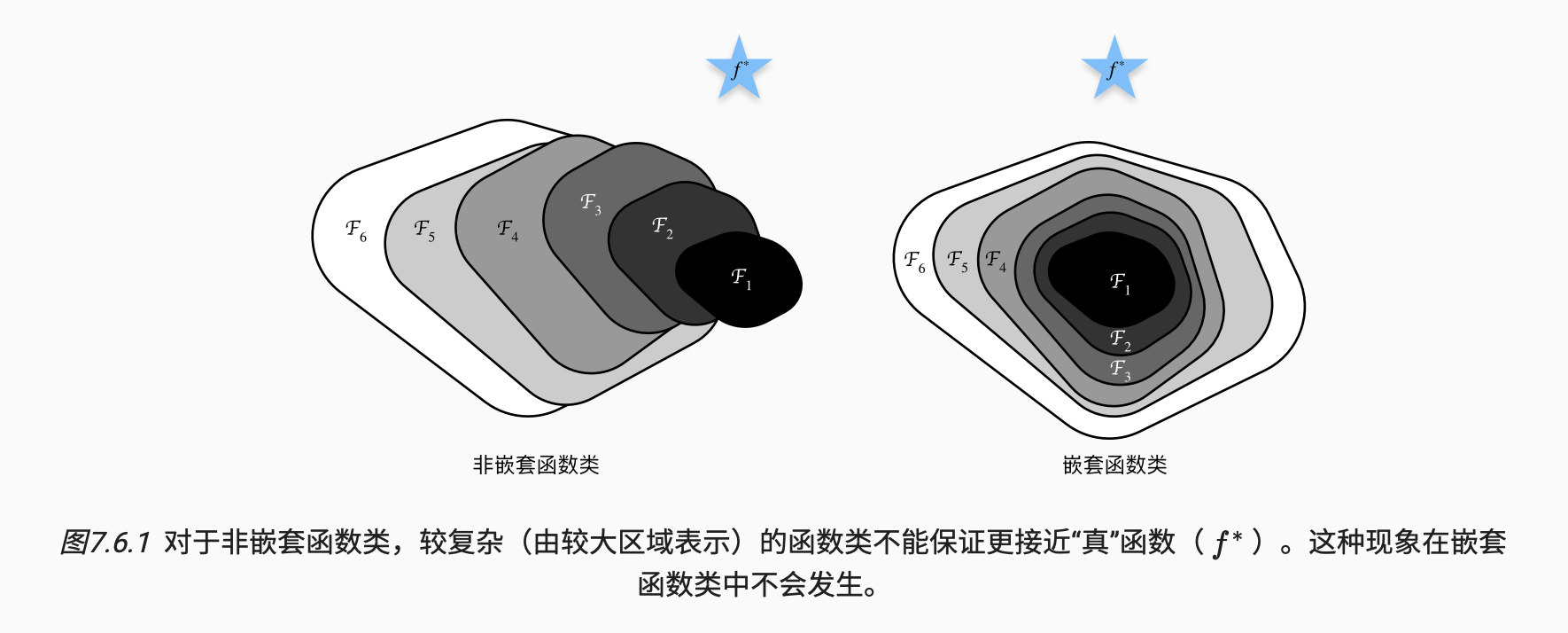
残差学习的数学原理

假设我们希望某几层堆叠学习到的理想映射为 $H(x)$。

传统方法：

• 直接让这几层拟合 $H(x)$
  残差学习方法：

• 让这几层拟合残差函数：$F(x) := H(x) - x$

• 原始映射变为：$H(x) = F(x) + x$
  为什么这样更好？

从优化角度看，假设理想映射接近恒等映射：

• 传统方法需要学习 $H(x) = x$，即多个非线性层拟合恒等映射（很难）
• 残差方法只需将 $F(x)$ 推向零（更容易）