Synergistic Information Distillation for Machine Learning

Synergistic Information Distillation (SID)

该算法通过协同信息蒸馏实现完全无反向传播的模块化训练，核心思想是将深度网络分解为多个独立优化的模块，每个模块通过局部目标函数逐步精炼”信念分布”。

网络架构

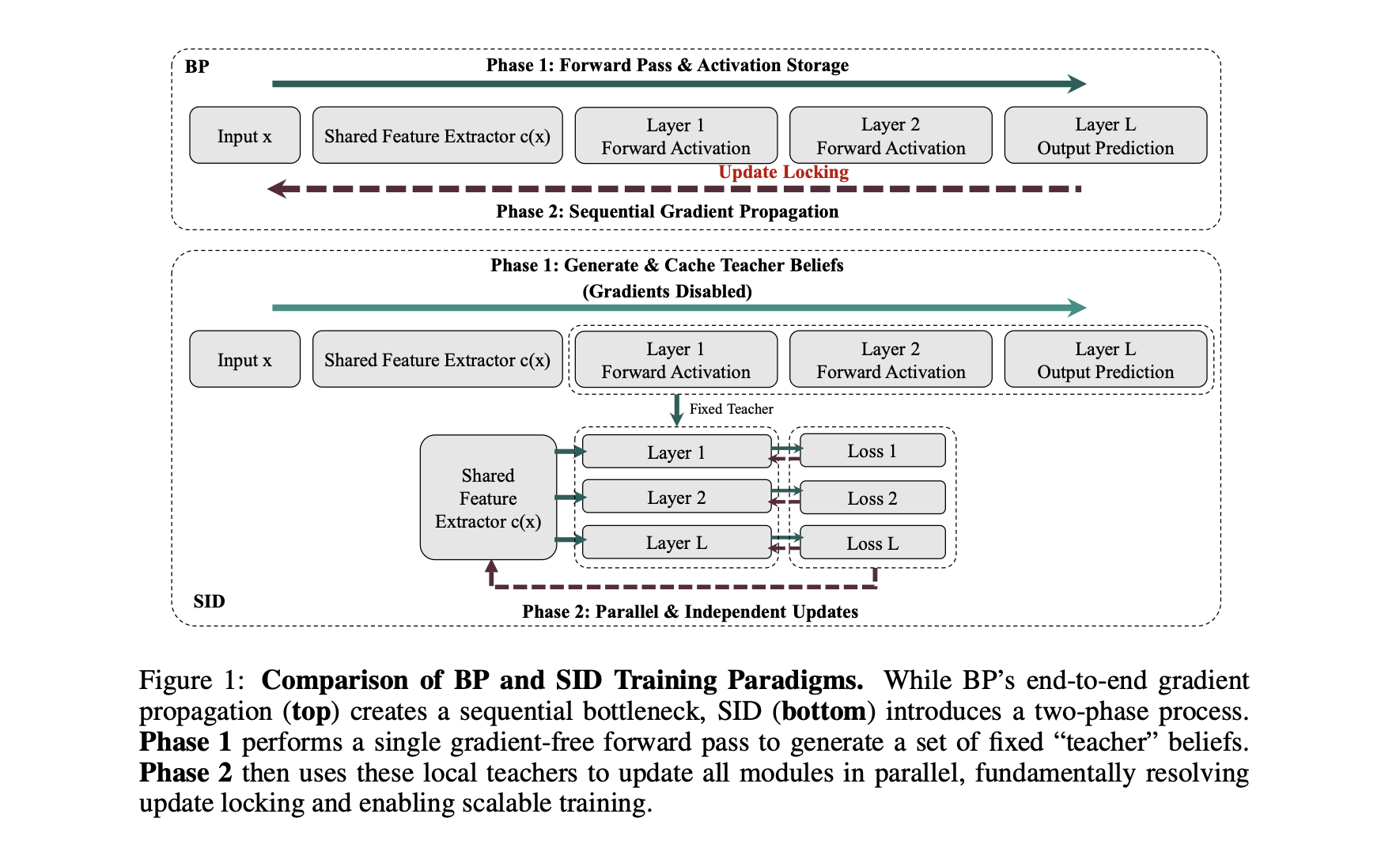
整体结构

text

输入 x
  ↓
共享特征提取器 c(x; θ_c): Conv层堆叠
  ↓ 输出特征 z ∈ R^d
  ├→ 模块 f_1(p_0, z; θ_1) → p_1
  ├→ 模块 f_2(p_1, z; θ_2) → p_2
  ├→ 模块 f_3(p_2, z; θ_3) → p_3
  └→ ...
     模块 f_L(p_{L-1}, z; θ_L) → p_L

变量说明：

• x: 输入数据（如图像）
• c(x; θ_c): 共享特征提取器，参数为 θ_c，输出特征向量 z
• f_i(·; θ_i): 第 i 个处理模块，参数为 θ_i
• p_i: 第 i 个模块输出的”信念分布”（概率向量），p_i ∈ R^N（N 为类别数）
• p_0: 初始均匀分布 Uniform(N)

  模块结构（典型实现）

text

输入: (p_{i-1}, z)
  ↓
Concat [p_{i-1}, z]  → 拼接向量 ∈ R^(N+d)
  ↓
Linear(θ_i)          → 线性变换
  ↓
Softmax              → 归一化为概率分布 p_i

形状变化：

• p_{i-1}: (batch, N)
• z: (batch, d)
• Concat: (batch, N+d)
• Linear: (batch, N+d) → (batch, N)
• p_i: (batch, N)

---

训练算法流程

SID采用两阶段训练机制，完全消除模块间的梯度依赖。

Phase 1: Teacher Beliefs 生成（无梯度）

目的：生成固定的”教师信念”作为一致性监督目标

with torch.no_grad():  # 关闭梯度计算
    # 1. 特征提取
    z_detached = c(x; θ_c)  # 共享特征（detached）

    # 2. 初始化均匀分布
    p_0 = Uniform(N)  # shape: (batch, N)

    # 3. 逐层前向传播
    P_teachers = [p_0]
    for i in 1 to L-1:
        p_i_teacher = f_i(P_teachers[i-1], z_detached; θ_i)
        P_teachers.append(p_i_teacher)

    # 4. 缓存教师信念
    return P_teachers  # [p_0, p_1^teacher, ..., p_{L-1}^teacher]

关键点：

• 整个过程不构建计算图
• 生成的 teacher beliefs 在 Phase 2 中视为常量

---

Phase 2: 并行模块更新（有梯度）

目的：各模块独立优化，共享特征累积所有模块梯度

# 1. 重新计算共享特征（带梯度）
z = c(x; θ_c)  # shape: (batch, d)

# 2. 并行计算各模块损失和梯度
gradients = {}
for i in 1 to L in parallel:  # 可在多GPU并行
    # 2.1 获取教师信念（常量）
    p_prev_teacher = sg(P_teachers[i-1])  # stop_gradient

    # 2.2 模块前向传播
    p_i = f_i(p_prev_teacher, z; θ_i)

    # 2.3 计算局部损失
    L_i = α · D_KL(p_i || p_y) + (1-α) · D_KL(p_i || sg(p_prev_teacher))

    # 2.4 计算梯度
    gradients[θ_i] = ∂L_i/∂θ_i        # 模块自身梯度
    gradients[θ_c] += ∂L_i/∂θ_c       # 累积到共享特征

# 3. 参数更新
for i in 1 to L:
    θ_i ← θ_i - η · gradients[θ_i]
θ_c ← θ_c - η · gradients[θ_c]

参数更新的数学表达式：

模块参数更新（各自独立）：

$$\theta_i^{(t+1)} = \theta_i^{(t)} - \eta \cdot \frac{\partial \mathcal{L}_i}{\partial \theta_i}$$

共享特征更新（累积所有模块梯度）：

$$\theta_c^{(t+1)} = \theta_c^{(t)} - \eta \cdot \sum_{i=1}^{L} \frac{\partial \mathcal{L}_i}{\partial \theta_c}$$

变量说明：

• sg(·): stop_gradient 算子，前向传值、反向截断梯度
• p_y: ground-truth 的 one-hot 编码
• α: 平衡超参数，控制蒸馏项与一致性项的权重
• D_KL(P||Q): KL散度，定义为 $\sum_k P(k) \log \frac{P(k)}{Q(k)}$
• η: 学习率

---

损失统计与更新

局部损失函数

数学定义：$\mathcal{L}_i(p_{i-1}; f_i) = \alpha \cdot D_{KL}(p_i | p_y) + (1-\alpha) \cdot D_{KL}(p_i | \text{sg}(p_{i-1}))$

两项作用：

Distillation Term（蒸馏项）：$ D_{KL}(p_i | p_y) = -\log p_i[y] $（$p_y $为 one-hot）

• 拉近模块输出与真实标签

• 提供主要的监督信号
  Consistency Term（一致性项）： $ D_{KL}(p_i | \text{sg}(p_{i-1})) = \sum_{k=1}^{N} p_i^{(k)} \log \frac{p_i^{(k)}}{p_{i-1}^{(k)}} $

• 防止当前模块过度偏离前序模块

• 正则化作用，保证渐进式优化
• sg() 阻断梯度：确保 $\frac{\partial \mathcal{L}_i}{\partial \theta_{i-1}} = 0$

---

Teacher Beliefs 的动态更新

Teacher beliefs 不是固定的预训练模型, 每个 batch 重新生成，随参数更新而改进

text

Iteration t:
  Phase 1: 用 θ^(t) 生成 P_teachers^(t)
  Phase 2: 用 P_teachers^(t) 更新参数 → θ^(t+1)

Iteration t+1:
  Phase 1: 用 θ^(t+1) 生成 P_teachers^(t+1)  ← 质量提升
  ...

---

梯度计算详解

共享特征梯度（长链，串行计算）

假设共享特征为 3 层：z = f_3(f_2(f_1(x; w_1); w_2); w_3)

模块 i 对各层的梯度：

$$\begin{aligned} \frac{\partial \mathcal{L}_i}{\partial w_3} &= \frac{\partial \mathcal{L}_i}{\partial p_i} \cdot \frac{\partial g_i}{\partial z} \cdot \frac{\partial f_3}{\partial w_3} \ \frac{\partial \mathcal{L}_i}{\partial w_2} &= \frac{\partial \mathcal{L}_i}{\partial p_i} \cdot \frac{\partial g_i}{\partial z} \cdot \frac{\partial f_3}{\partial h_2} \cdot \frac{\partial f_2}{\partial w_2} \ \frac{\partial \mathcal{L}_i}{\partial w_1} &= \frac{\partial \mathcal{L}_i}{\partial p_i} \cdot \frac{\partial g_i}{\partial z} \cdot \frac{\partial f_3}{\partial h_2} \cdot \frac{\partial f_2}{\partial h_1} \cdot \frac{\partial f_1}{\partial w_1} \end{aligned}$$

累积所有模块的梯度：

$$\frac{\partial \mathcal{L}_{\text{total}}}{\partial w_1} = \sum_{i=1}^{L} \frac{\partial \mathcal{L}_i}{\partial w_1}$$

关键点: $\sum_i \frac{\partial \mathcal{L}_i}{\partial z}$ 可并行计算,但 $\frac{\partial f_3}{\partial h_2} \cdot \frac{\partial f_2}{\partial h_1} \cdot \frac{\partial f_1}{\partial w_1}$ 必须串行, 这部分复杂度与 BP 相同

---

模块参数梯度（短链，可并行）

$$\frac{\partial \mathcal{L}_i}{\partial \theta_i} = \frac{\partial \mathcal{L}_i}{\partial p_i} \cdot \frac{\partial p_i}{\partial \theta_i}$$

特点：

• 梯度链路短（仅通过单个模块）
• 完全独立，可在多 GPU 并行计算

  text

  1. 计算 z = c(x; θ_c^(t))  ← θ_c 固定在当前值
  2. 并行计算（θ_c 不变）：
     GPU 1: z → p_1 → L_1 → ∂L_1/∂θ_c
     GPU 2: z → p_2 → L_2 → ∂L_2/∂θ_c
     GPU 3: z → p_3 → L_3 → ∂L_3/∂θ_c
  3. 汇总：g_c = Σ ∂L_i/∂θ_c
  4. 更新：θ_c ← θ_c - η · g_c

时间复杂度

• 传统 BP（单分类头）： $ T_{BP} = T_{\text{feat fwd}} + T_{\text{cls fwd}} + T_{\text{cls bwd}} + T_{\text{feat bwd}} $
• SID（多模块）： $ T_{SID} = T_{\text{feat fwd}} + \max_i T_{g_i \text{ fwd}} + \max_i T_{g_i \text{ bwd}} + T_{\text{feat bwd}} $
• 理论加速：如果 $\max_i T_{g_i} < T_{\text{单分类头}}$，可能更快，但增加了额外模块计算，未必总是更快
  论文实测：在理想并行条件下，加速 2-3倍

---

内存复杂度

BP 内存需求： $ M_{BP} \approx \sum_{i=1}^{L} A_i \quad \text{（存储所有层激活）} $

SID 内存需求： $ M_{SID} \approx \max_i A_i + \sum_{i=0}^{L-1} |p_i| \quad \text{（单模块激活 + teacher beliefs）} $

实际节省：

• CIFAR-100 实验：150 MB → 1.25 MB

• 节省 120 倍
  原因：

• Teacher beliefs 只是概率向量（小）

• 只需存储当前模块激活
• 不需要存储中间层的完整特征图

---

收敛性保证

理论保证（Proposition 2）： $ D_{KL}(p_L | p_y) \leq D_{KL}(p_0 | p_y) - \frac{1-\alpha}{\alpha} \sum_{i=1}^{L} D_{KL}(p_i | p_{i-1}) $

最终预测与真实标签的距离 ≤ 初始距离 - 累积改进量，所以只要每层满足 $\mathcal{L}_i(p_i) \leq \mathcal{L}_i(p_{i-1})$（局部改进）就能保证全局性能单调不退化

• Distillation：向正确答案靠近
• Consistency：不偏离前序信念太远
• 两者平衡 → 稳定收敛

---